Operaciones entre números complejos

En esta página vamos a explicar cómo sumar, restar, multiplicar y dividir números complejos.

Índice de contenidos:

Sumar y restar en forma binómica
Multiplicar y dividir en forma binómica
Multiplicar y dividir en forma polar

Otros temas de números complejos:

1. Sumar y restar en forma binómica

Sean $z$ y $w$ dos complejos dados en su forma binómica:

Explicamos y damos las fórmulas para sumar, restar, multiplicar y dividir números complejos o imaginarios en su forma binómica y en su forma polar. Incluye ejemplos y enlaces de interés. Matemáticas. Números complejos. Secundaria. Bachillerato. Universidad.

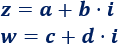
La suma de los complejos $z$ y $w$ es un número complejo cuya parte real es la suma de las partes reales y cuya parte imaginaria es la suma de las partes imaginarias:

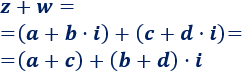
La resta es análoga, pero restando:

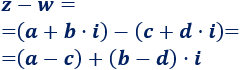
Problema 1

Sumar y restar los siguientes números complejos:

Calculamos la suma $z + w$ :

Calculamos la resta $z - w$ :

Comentarios

Entradas populares de este blog

Análisis de velocidad de un mecanismo RRRP usando polígono de velocidad

Considere el mecanismo de la FIgura 1.

My University World

TÉCNICAS DE ESTUDIO ¿Qué son las técnicas de estudio y para qué s irven? Las técnicas de estudio son estrategias o recursos que facilitan la adquisición de conocimientos. Se utilizan para aprender mejor y de manera más eficaz con el objetivo de conseguir un mayor rendimiento académico. Establece objetivos Antes de empezar a definir tu plan de estudio, es necesario establecer unos objetivos de aprendizaje . Tener unas metas específicas y medibles es el primer paso y el más importante en tu planificación. Considera todas las actividades que realizas en tu día a día Sé realista y ten en cuenta el tiempo que inviertes en otras actividades como hacer deporte, estar con tu familia o amigos, comer o dormir. Puedes reconsiderar el tiempo dedicado a estas actividades en función de tus prioridades. Fija un horario dedicado al estudio Una vez hayas definido esos horarios, señala el periodo de tiempo que d...