¿Cuáles son las Leyes de Newton?

 Recordad que un complejo en (forma binómica) es 

$z=a+b\cdot i$, siendo $a$ y $b$ números reales. La parte real del complejo $z$ es $Re\left(z\right)=a$ y la parte imaginaria es $Im\left(z\right)=b$.

Los complejos se representan en el plano complejo, que es como el plano cartesiano. El complejo $z=a+b\cdot i$ se representa como el vector $(a,b)$ en el plano real:

Es decir, la primera coordenada del vector es la parte real y la segunda coordenada es la parte imaginaria.

Forma polar de un complejo

Si vemos los complejos como vectores, es lógico pensar en su módulo $r=|z|$ (longitud del vector) y en el ángulo $\alpha$ que forma el vector con el eje real.

La forma trigonométrica de un complejo $z$ con módulo $r$ y ángulo $\alpha$ es

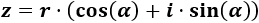
La forma polar de un complejo es cualquiera de las siguientes:

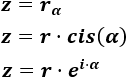
Para pasar de la forma polar a la binómica, utilizamos la forma trigonométrica (calculando el seno y el coseno del ángulo).

Veamos ahora cómo se definen y calculan el módulo y el ángulo:

El módulo de un complejo $z=a+b\cdot i$ se representa por $|z|$ y se define como

$$|z|=\sqrt{a^2+b^2}\ge 0$$

El ángulo $\alpha$ de $z$ se calcula con la función inversa de la tangente:

$$\alpha =atan\left(\frac{b}{a}\right)$$

Nota: cuando el complejo está sobre el eje vertical o es nulo, es decir, si $a=0$, entonces el ángulo es

• $\alpha =\pi /2$ (90 grados) si $b>0$,
• $\alpha =-\pi /2$ (-90 grados) si $b<0$ y
• $\alpha =0$ si $b=0$.

Además de esto, la función arcotangente proporciona ángulos entre $-\pi /4$ y $\pi /4$. Así que,

• Si el complejo está en el segundo cuadrante ($a<0$, $b>0$), hay que sumar $\pi$ al ángulo obtenido.

• Si el complejo está en el tercer cuadrante ($a<0$, $b<0$), hay que restar $\pi$ al ángulo obtenido.

Recordad que un vector con módulo $|z|$ y ángulo $\alpha$ es equivalente al vector con el mismo módulo y ángulo $\alpha +2k\pi$. Es por esta razón por la que se define el argumento principal:

El argumento principal de $z$ se representa por $Arg\left(z\right)$ y es el ángulo de $z$ equivalente en el intervalo $\left]-\pi ,\pi \right]$.

Producto y cociente en forma polar

La forma polar nos permite calcular el producto y el cociente de dos complejos muy rápidamente por las propiedades de las potencias.

Consideremos los complejos $z_1=r_1\cdot e^{i\cdot \alpha }$ y $z_2=r_2\cdot e^{i\cdot \beta }$.

Calculamos su producto:

Nota: si trabajamos con la forma polar que no utiliza la exponencial, no importa:

El producto de los complejos tiene módulo $r=r_1\cdot r_2$ y ángulo $\alpha +\beta$.

Calculamos su cociente:

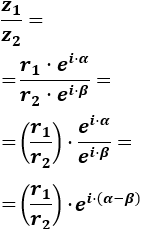
El cociente de los complejos tiene módulo $r=r_1\cdot r_2$ y ángulo $\alpha -\beta$.